No, engineers don’t suck at time estimates - and generally speaking humans are better estimators than what most people believe. This seems rather surprising given all we’ve heard about the problems of bad time estimations, projects going overboard, etc and of course, your personal experience with software time estimates. But if people are really bad at estimation, how does that fit with our obvious evolutionary need to make quick decisions based on partial data? if we can’t estimate well how did we decide if a gap is wide enough to jump over, if an animal is worth the hunt, if a certain area is more likely to have water and shade? Without estimation skills we wouldn’t survive. So what’s going on?

One obvious explanation is that we are only good at estimating physical things such as sizes and distances. However, this does not seem likely given the large number of non-physical decisions we needed to make, like selecting a mate. Another, more likely explanation is that the estimates are good, but the interpretation and usage of the estimates is flawed. In other (slightly cynical) words: the engineers are good at estimating, it’s the project managers who suck at using the estimates.

Let me explain.

What is an estimate?

“your estimate was wrong” - is something i’ve heard many times. But this sentence doesn’t make any sense… after all, an estimate is by definition not exact; in fact, if the results would always agree with estimates foul play would be immediately suspected. If I estimated one day and the actual time was 1.5 days, was I “wrong”? most people would say I wasn’t. But if if the actual time was 20 days most people would argue I was wrong. Somewhere between one and 20 days there is an implicit “reasonable error” threshold we never discussed! I never gave an error margin for my estimate, did I?

Since we don’t expect an estimate to be an exact guess of the actual value, what do we expect from an estimate? When we make decisions based on estimates, we can only be right or wrong in our decision, you can’t be “a lot more right”. We need to guess a value beyond a certain threshold and within a certain tolerance, with high probability of being right because that our lives depend on that gap being just short enough for us to jump over. Decisions are almost always non-linear like that and it should not be surprising given the nature of knowledge and learning. We take in examples and extrapolate patterns and behaviors. Which means we are dealing with groups, and probability distributions. This may be surprising at first, because when you are estimating this one particular job, you don’t think of a distribution of a million other different jobs. An estimate is predicting the future in which we see the actual value.

What we need to know, is that in a certain number of futures, say 90% of them, a value won’t be over or under a certain threshold. Or phrased mathematically, that the 90th percentile of the distribution of futures will be over (or under) a certain number. An estimate is a percentile! but which percentile? is it the median? the 99th? For software time estimates it has been observed to be the median (50th percentile), meaning to be right about half the times. Is this inherent? Estimates can demonstrably be calibrated to higher percentiles by as little as brief emotional self manipulation; You could easily estimate the 90th percentile of many things - just read How to measure anything.

Usually when I tell this to people, they often respond with “we’ll train to estimate the average”. Sadly, this is not possible. The mean is a statistically “unstable” or “unrobust” aggregate, where as percentiles are “stable” or “robust”. Consider a group of task completion times [73, 67, 12, 38, 18, 11, 42]. The mean is ~37.29 and the median is pretty close, 38. But as soon as we get another measurement, say 293, the mean changes significantly to 69.25 while the median changes only slightly to 42. The mean is sensitive to outliers, and the more skewed and high variance the distribution the less robust and stable it will be.

You had one job

Having estimated tasks, what do we do with them? We sum them up.

Either for project budget or for by enqueuing with the next tasks, we sum them. But wait, we know that percentiles are not additive! how can this ever work? it never does. Summing up percentiles compounds errors and with skewed distributions, and in particular heavy tailed distributions, the errors are very large. Let’s have a look at what a task completion time distribution would look like: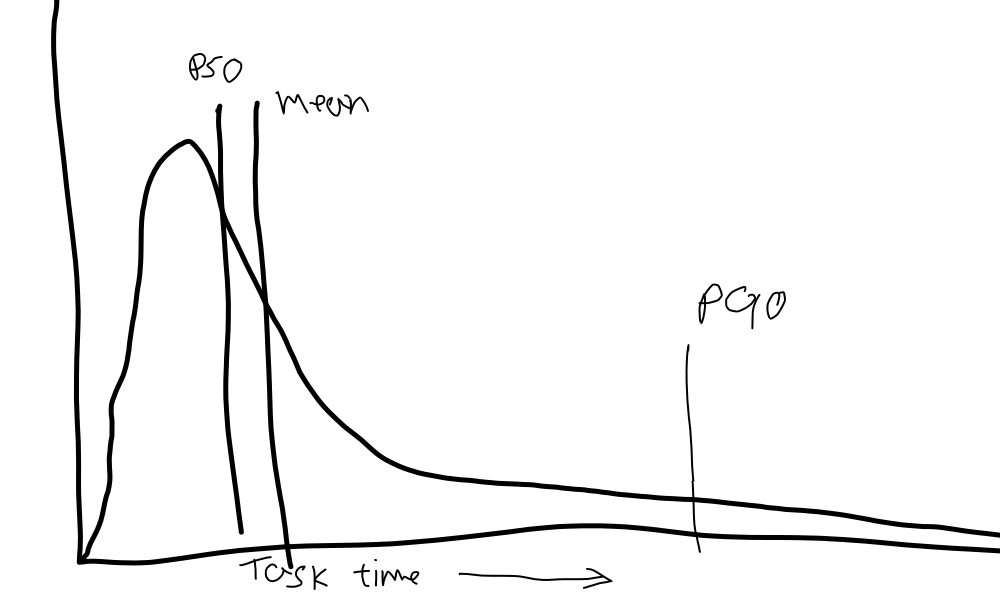

A task has some minimum time it has to take, but beyond that it can pretty much take as long as infinity. We all know from experience, that when things get out of control they go wayyyy out of control. Once you hit a rare bug, you might be chasing a wild goose for two months. That 10% over the estimate might be a day late or a year, the higher percentile you pick the more extreme the errors relatively.

To be honest, it’s old news; This has been known for a long time. Percentile based project predictions have been done as early as World War II, perhaps even before that - yet they remain fairly unknown in the industry. Not only are we ignorant of proven methods, we invent new ones which are outright harmful. Remember that burn down chart? the backlog is nothing more than a sum of time estimates! And every two weeks, sitting in the famous sprint retrospective people work to calibrate their estimates to the random walk sum of task completion times on the burndown chart. How do you calibrate a percentile to a sum? If the distribution is something like a log-normal distribution, the random walk sum will converge to the mean, and the median is relatively close to the mean - which is summable, and both are pretty stable. So by repeatedly calibrating estimates to the running-sum of task completion times (the backlog) you will converge close to the median. Now go tell your project manager there is a 50% chance of their project running late, anywhere between a day and eternity, and see how they respond. A 50% chance of uncapped delay is a useless estimate.

Scrum is a training method for useless time estimates. It actively destroys your ability to manage your project.

Don’t get me wrong, I’m not against Agile; The spirit of Agile, some of the methods and ceremonies of Scrum have value. But Scrum as a system is actively harmful, especially in high variance situations where the work is far from the nice log-normal distribution. If you optimize for an arbitrary metric, you will get arbitrary results. In ops/SRE and pure research many people have intuitive sense that Scrum and traditional project management are wrong, although they can’t quite articulate why. The reasons become very clear when we consider what happens to sum based project management methods if the task distribution becomes heavy tailed. A task that is one week late is likely to take at least one more week - is a common thumb rule in such domains; This is called a “Power law” and can be modeled by the famous Pareto distribution. The thing about the Pareto distribution is that its mean does not converge¹! In other words, using sum based planning methods with such distributions is equivalent to managing by rolling dice. A little worse actually, as dice are a cheap method of generating random numbers where as time estimates are intrusive and sometimes expensive. This isn’t a problem unique to Scrum, nor does it originate from it. The problem is the assumption of determinism and accuracy which is the prevailing “machine age” mindset. Pretty much all of the common project management tools have the same issue - have a look at a Gantt chart, it has no probability intervals or error ranges. They are all worse than useless. It shouldn’t be a surprise that despite people being bad at estimating large tasks naive estimates are reliably more accurate than project management tools.

Managing uncertainty

Recognizing the probabilistic nature of the world is key. Probability isn’t a tool for making predictions, it is a tool for quantifying uncertainty. Instead of managing resources (which are usually highly certain) we should be managing uncertainty, with probabilistic methods appropriate for the task. With this mindset, the first thing to do is understand the business context and the distributions involved: are you in a low or high variation domain? Industrial methods which aim to improve throughput and efficiency all assume low variance, sometimes actively force low variance by getting rid of outliers; this isn’t necessarily possible in your business context. Industrial methods are good when used in context, but horrible when used in high variability and unpredictable domains. For those we have other methods, which emphasize low latency and rapid adaptation. Instead of Scrum, you could try:

• Monte-Carlo simulations based on time estimates
• Time boxing and bets
• Latency optimizing methods which dispense with time estimates, like Kanban

I’ve listed the methods above in order of rising uncertainty, Monte-Carlo simulations or time boxing would probably be easiest to start with. The biggest obstacle in implementing these is convincing managers that “predictability” isn’t so important as they imagine. For high variation domains it’s nothing more than a fantasy anyway.

So there you have it: people don’t suck at estimation. They suck at management 🤷